Prime Numbers:
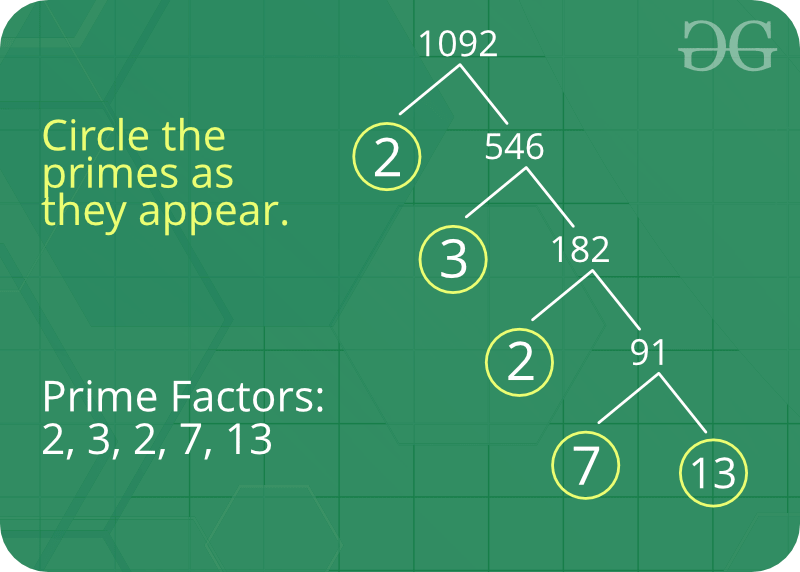
Divisibility:
The prime number law stated above means that, in order for a number x to divide a number y (written x/y, or mod(y, x) = 0), all primes in x's prime factorization must be in y's prime factorization. Or, more specifically,
Let x =
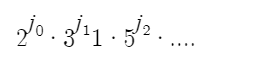
Let y =
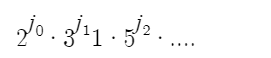
if x/y, then for all I, ji <= ki.
In fact, the greatest common divisor of x and y will be:
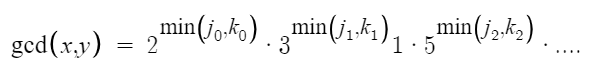
The least common multiple of x and y will be
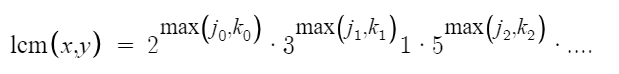
Checking for Primality:
- This question is so common that we feel the need to specifically cover it. The naive way is to simply iterate from 2 through n-1, checking for divisibility on each iteration.
boolean primeNaive(int n) {
if (n < 2){
return false;
}
for (int i = 2; i < n; i++){
if (n % i == 0){
return false;
}
}
return true;
}This can be improved through the square root of n.
boolean primeSlightlyBetter(int n){
if (n < 2){
return false;
}
int sqrt = (int) Math.sqrt(n);
for (int i = 2; i <= sqrt; i++){
if (n % i == 0) return false;
}
return true;
}
Generating a List of Primes
The sieve of Eratosthenes is a highly efficient way to generate a list of primes. It works by recognizing that all non-prime numbers are divisible by a prime number.
We start with a list of all the numbers up through some value max. First, we cross off all numbers divisible by 2. Then, we look for the next prime (the next non-crossed-off number) and cross off all numbers divisible by it. By crossing off all numbers divisible by 2,3, 5, 7, 11, and so on, we wind up with a list of prime numbers from 2 through max.
The code below implements the Sieve of Eratosthenes.
boolean[] sieveOfEratosthenes(int max) {
boolean[] flags = new boolean[max + 1];
int count = 0;
init(flags); // Set all flags to true other than 0 and 1
int prime = 2;
while (prime <= Math.sqrt(max)){
/* Cross off remaining multiples of prime */
crossOff(flags, prime);
/* Find next value which is true */
prime = getNextPrime(flags, prime);
}
return flags;
}
void crossOff(boolean[] flags, int prime){
/* Cross off remianing multiples of prime. We can start with (prime * prime),
* because if we have a k * prime, where k < prime, this value would have
* already been crossed off in a prior iteration */
for (int i = prime * prime; i < flags.length; i+= prime){
flags[i] = false;
}
}
int getNextPrime(boolean[] flags, int prime) {
int next = prime + 1;
while (next < flags.lenght && !flags[next]){
next++;
}
return next;
}Probability:
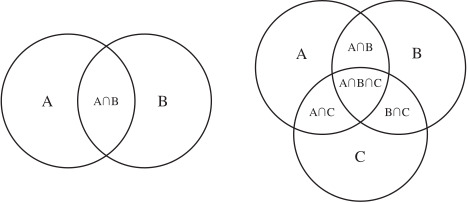
Probability of A and B
Imagine you were throwing a dart at this Venn diagram. What is the probability that you would land in the intersection between A and B? If you knew the odds of landing in A, and you also knew the percent of A that's also in B. Then you would express the probability as:
P(A and B) = P(B given A) P(A)
For instance, picking a number between 1 and 10. The probability of picking a number that is both even and between 1 and 5 is 50%. The odds of a number between 1 and 5 being even is 40%. So the odds of doing both are:
P(x is even and x <= 5) = P( x is even given x <= 5) P(x<=5)
= (2/5) * (1/2)
= 1/5
Observe that since P(A and B) = P(B given A) P(A) = P(A given B) P(B), you can express the probability of A given B in terms of the reverse.
P(A given B) = P(B given A) P(A) / P(B)
The above equation is called Bayes' Theorem.
Probability of A or B
P(A or B) = P(A) + P(B) - P(A and B)
Logically, this makes sense. If we simply added their sizes, we would have double-counted their intersection. We need to subtract this out.
P(x is even or x <= 5)
= P(x is even) + P(x <= 5) - P(x is even and x <=5)
= 1/2 + 1/2 - 1/5
= 4/5
Independence
If A and B are independent ( that is, one happening tells you nothing about the other happening),
then, P(A and B) = P(A) P(B). This rule simply comes from recognizing that P(B given A) = P(B), since A indicates nothing about B.
Mutual Exclusivity
If A and B are mutually exclusive (that is, if one happens, then the other cannot happen, then P(A or B) = P(A) + P(B). This rule simply comes from recognizing that P(B given A) = P(B), since A indicates nothing about B.
There cannot be both mutually exclusive and independent.
In these kinds of questions:
Develop Rules and Patterns:
- Write those patterns and rules.
Worst Case Shifting
- Worst-cast minimization problems, worded either in terms of minimizing an action or in doing something at most a specific number of times. A useful technique is to try to "balance" the worst case. That is, if an early decision results in a skewing of the worst case, we can sometimes change the decision to balance out the worst case.
'Algorithms and Data Structures > Algorithms' 카테고리의 다른 글
| LeetCode 278. First Bad Version (0) | 2022.06.15 |
|---|---|
| Bit Manipulation (0) | 2022.06.11 |
| How to Optimize Solutions for Coding Problems (0) | 2022.05.17 |
| [Coding Test] How to Solve Coding Problems (0) | 2022.05.15 |
| [Big O] Missed Questions (0) | 2022.05.14 |