Min Heap: A complete binary tree (that is filled other than the rightmost elements on the last level) where each node is smaller than its children. The root, therefore, is the minimum element in the tree.
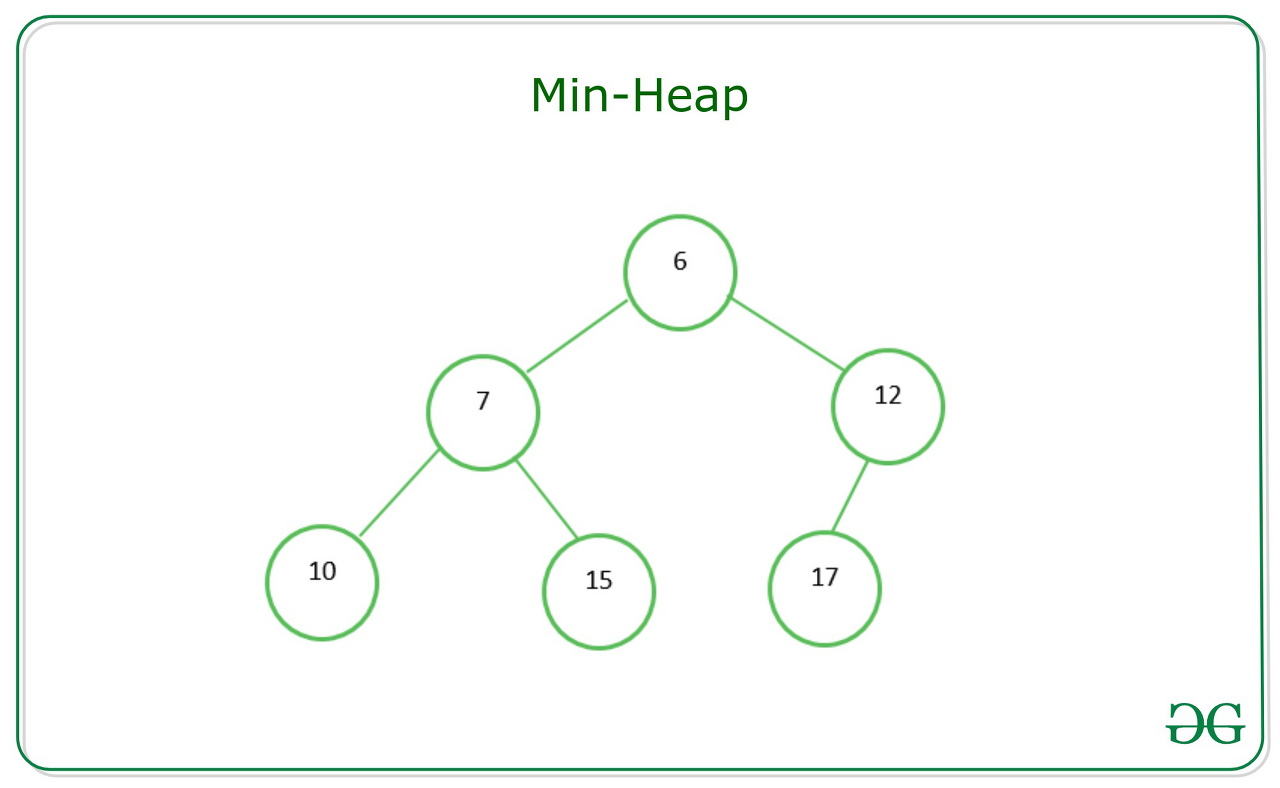
We have two key operations on a min-heap: insert and extract_min
Insert
When we insert into a min-heap, we always start by inserting the element at the bottom. We insert it at the rightmost spot to maintain the complete tree property.
Then, we "fix" the tree by swapping the new element with its parent until we find an appropriate spot for the element. We essentially bubble up the minimum element.
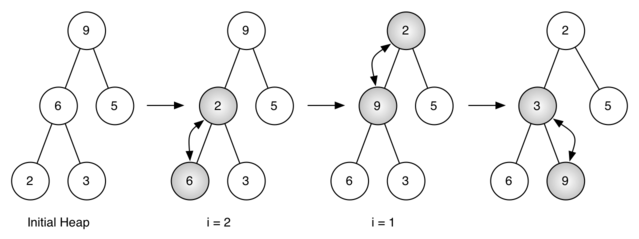
It takes O(log n) time, where n is the number of nodes in a heap.
Extract Minimum Element
Finding the minimum element of a min-heap is easy: it's always at the top. The trickier parit is how to remove it. (In fact, this isn't that tricky.)
First, we remove the minimum element and swap it with the last element in a heap (the bottommost, rightmost element) Then, we bubble down this element, swapping it with one of its children until the min-heap property is restored.
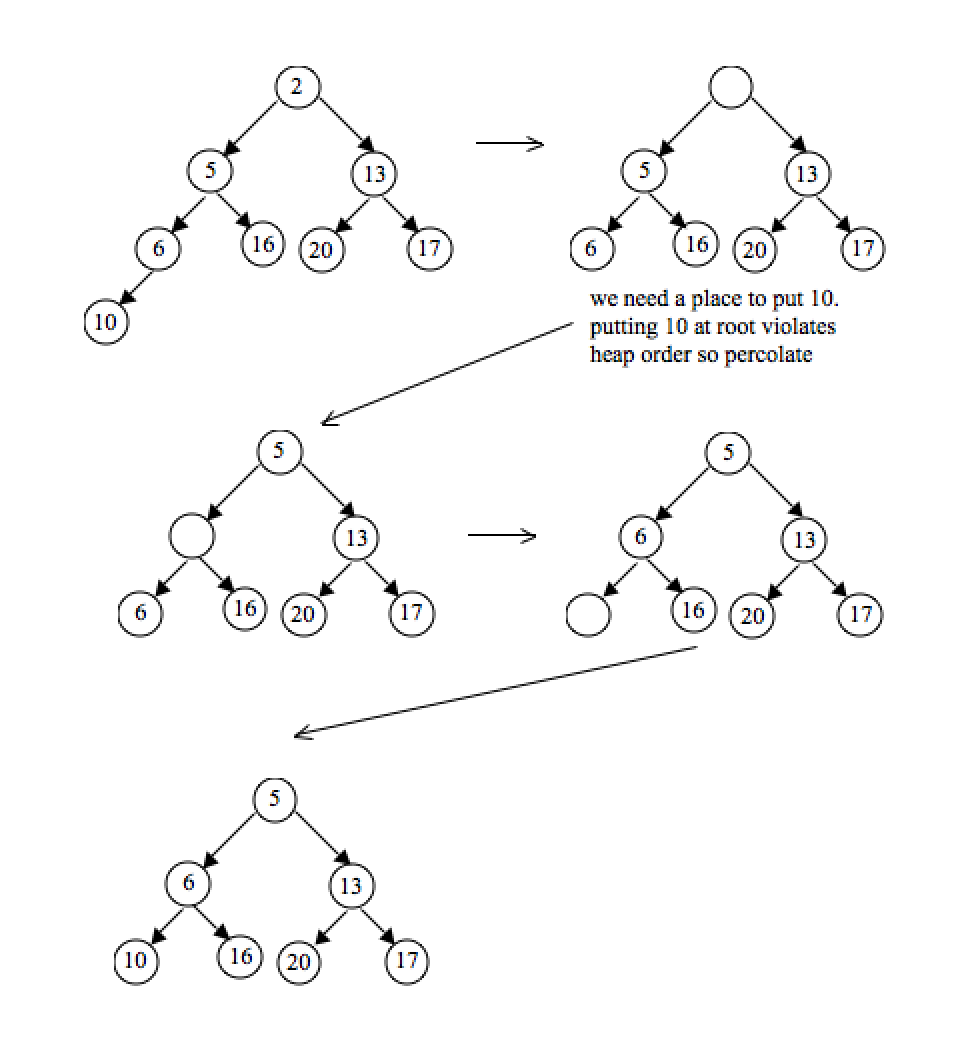
Do we swap it with the left child or the right child? That depends on their values. There's no inherent ordering between the left and right elements, but you'll need to take the smaller one to maintain the min-heap ordering.
This algorithm will also take O(log n) time.
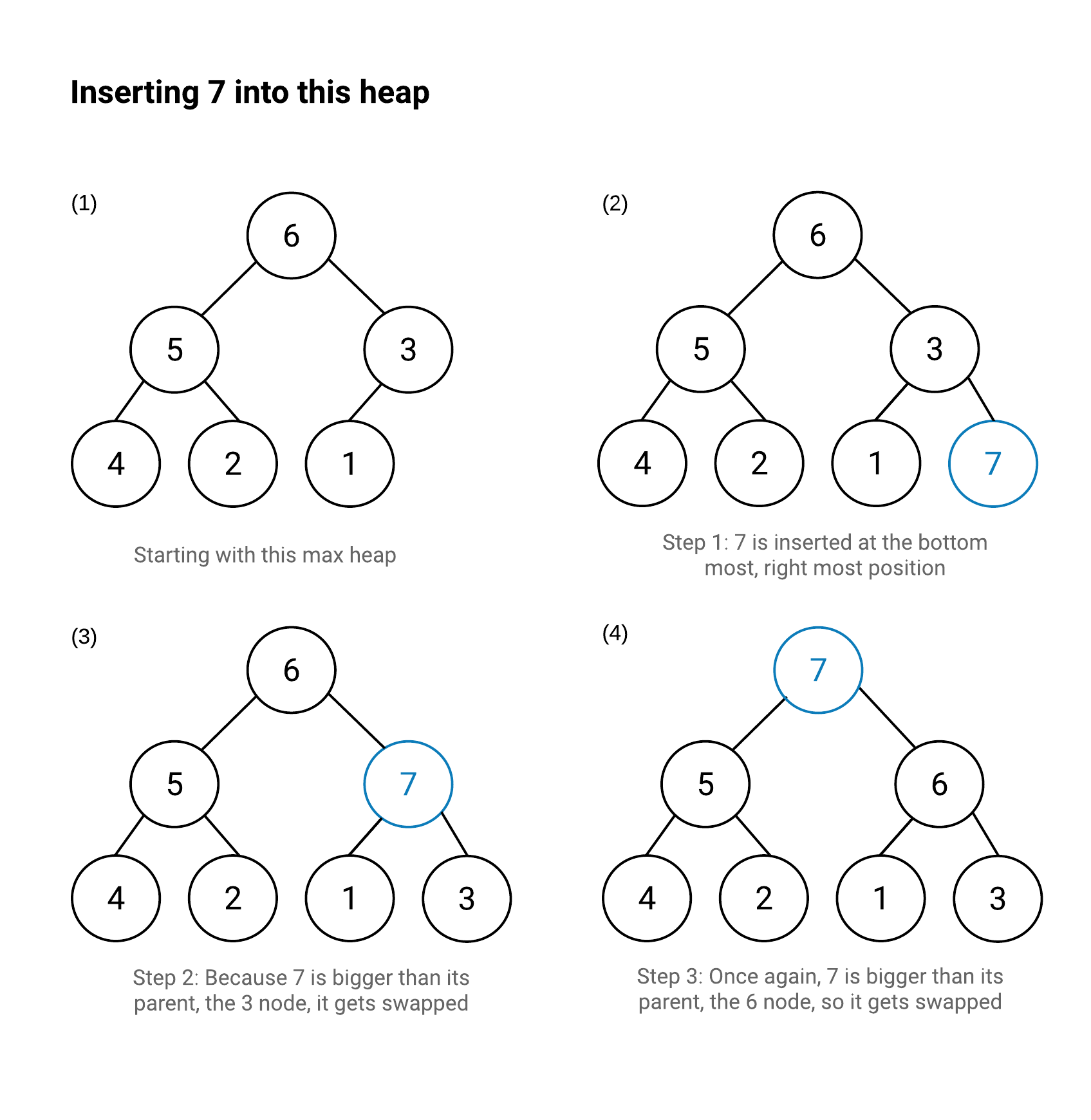
Max heap Insertion Process:
'Algorithms and Data Structures > Data Structures' 카테고리의 다른 글
| [Data Structures] Graphs (0) | 2022.05.28 |
|---|---|
| [Data Structures] Tries (Prefix Trees) (0) | 2022.05.27 |
| [Data Structures] Binary Tree Traversals with Implementations (0) | 2022.05.25 |
| [Data Structures] Trees (BT, BST) (0) | 2022.05.24 |
| [Data Structures] Stacks and Queues (0) | 2022.05.22 |