The two most common ways to search a graph are depth-first search and breadth-first search.
In depth-first search (DFS), we start at the root (or another arbitrarily selected node) and explore each branch completely before moving on to the next branch. That is, we go deep first (hence the name depth-first search) before we go wide.
In breadth-first search (BFS), we start at the root (or another arbitrarily selected node) and explore each neighbor before going on to any of their children. That is, we go wide (hence breadth-first search) before we go deep.
See the below depiction of a graph and its depth-first and breadth-first search (assuming neighbors are iterated in numerical order)
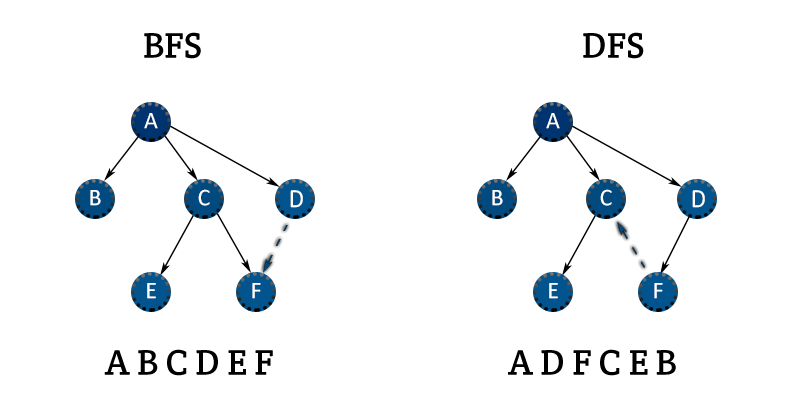
Breadth-first search and depth-first search tend to be used in different scenarios. DFS is often preferred if we want to visit every node in the graph. Both will work just fine, but depth-first search is a bit simpler.
However, if we want to find the shortest path between two nodes, BFS is generally better. Consider representing all the friendships in the entire world in a graph and trying to find a path of friendships between Ash and Vanessa.
In depth-first search, we could take a path like Ash -> Brian -> Carleton -> ... and then find ourselves very far away. We could go through most of the world without realizing that, in fact Vanessa is Ash's friend. We will still eventually find the path, but it may take a long time. It also won't find us the shortest path.
In the breadth-first search, we would stay close to Ash for as long as possible. We might iterate through many of Ash's friends, but we wouldn't go to his more distant connections until absolutely necessary. If Vanessa is Ash's friend, or his friend-of-a-friend, we'll find this out relatively quickly.
void DFS_Search(Node root) {
if (root == null) return;
visit(root);
root.visited = true;
for each (Node n in root.adjacent) {
if (n.visited == false) {
search(n);
}
}
}
void BFS_Search(Node root) {
Queue queue = new Queue();
root.marked = true;
queue.enqueue(root); // Add to the end of queue
while (!queue.isEmpty()) {
Node r = queue.dequeue(); // Remove from the front of the queue
visit(r);
foreach (Node n in r.adjacent) {
if (n.marked == false) {
n.marked = true;
queue.enqueue(n);
}
}
}
}'Algorithms and Data Structures > Data Structures' 카테고리의 다른 글
| Object-Oriented Design (0) | 2022.06.24 |
|---|---|
| [Data Structures] Graphs (0) | 2022.05.28 |
| [Data Structures] Tries (Prefix Trees) (0) | 2022.05.27 |
| [Data Structures] Binary Heaps (Min-Heaps and Max-Heaps) (0) | 2022.05.26 |
| [Data Structures] Binary Tree Traversals with Implementations (0) | 2022.05.25 |